知识储备
1.平行四边形的面积公式是S=底×高;
2.等面积法:将同一图形或相等面积的图形的面积用不同的方法表示出来从而得到等式,建立方程解决问题的方法。
3.由习题总结的规律:若一条直线经过平行四边形对角线的交点,则这直线平分平行四边形的周长和面积;
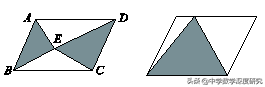
4.基础图形及结论:图形中阴影部分的面积是平行四边形面积的一半

分类解析
类型1 数形互助
1.如图是一个由5张纸片拼成的平行四边形,相邻纸片之间互不重叠也无缝隙,其中两只等腰直角三角形纸片的面积都为m,另两张直角三角形纸片的面积都为n,中间一张正方形纸片的面积为1,则这个平行四边形的面积一定可以表示为( )
A.4mB.4nC.4n+1D.3m+4
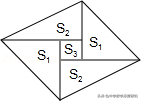
【分析】设等腰直角三角形的直角边为a,正方形边长为c,求出S2(用a、c表示),得出S₁,S₂,S₃之间的关系,由此即可解决问题.
【解答】设等腰直角三角形的直角边为a,正方形边长为c,
则S₂=1/2(a+c)(a﹣c)=1/2a²﹣1/2c²,
∴S₂=S₁﹣1/2S₃, ∴S₃=2S₁﹣2S₂,
∴平行四边形面积=2S₁+2S₂+S₃=2S₁+2S₂+2S₁﹣2S₂=4S₁=4m,
故选:A.
【点评】本题考查平行四边形的性质、直角三角形的面积等知识,解题的关键是求出S₁,S₂,S₃之间的关系,属于中考常考题型.

类型2 等面积法
2.如图,已知平行四边形ABCD中,AE⊥BC于E,AF⊥CD于F,如果AE=3cm,AF=4cm,▱ABCD周长是28cm,求▱ABCD的面积.
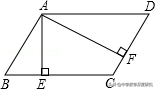
【分析】由▱ABCD中,AE⊥BC于E,AF⊥CD于F,可得S▱ABCD=BC•AE=CD•AF,又由AE=3cm,AF=4cm,可得3BC=4CD,又由▱ABCD的周长为28cm,可得BC+CD=14cm,继而求得答案.
【解答】∵▱ABCD的周长为28cm,∴BC+CD=14cm,
∵▱ABCD中,AE⊥BC,AF⊥CD,
∴S▱ABCD=BC•AE=CD•AF
∵AE=3cm,AF=4cm,∴3BC=4CD,
∴BC=8cm,CD=6cm,
∴ABCD的面积=8×3=24cm2.
【点评】此题考查了平行四边形的性质以及平行四边形的面积公式运用,此题难度适中,注意掌握方程思想与数形结合思想的应用.

3.我们知道:平行四边形的面积=(底边)×(这条底边上的高).
如图,四边形ABCD都是平行四边形,AD∥BC,AB∥CD,设它的面积为S.
(1)如图①,点M为AD上任意一点,则△BCM的面积S1= S,
△BCD的面积S₂与△BCM的面积S₁的数量关系是________ .
(2)如图②,设AC、BD交于点O,则O为AC、BD的中点,试探究△AOB的面积与△COD的面积之和S₃与平行四边形的面积S的数量关系.
(3)如图③,点P为平行四边形ABCD内任意一点时,记△PAB的面积为Sˊ,△PCD的面积为S″,平行四边形ABCD的面积为S,猜想得Sˊ、S″的和与S的数量关系式为 .
(4)如图④,已知点P为平行四边形ABCD内任意一点,△PAB的面积为3,△PBC的面积为7,求△PBD的面积.
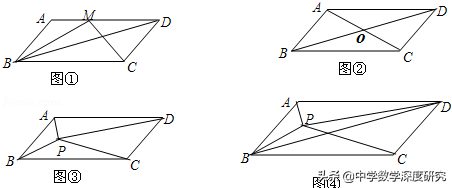
【分析】(1)设▱ABCD中BC边上的高为h₁,CD边上的高为h₂,再根据平行四边形的面积与三角形的面积公式求解即可;
(2)根据O为AC、BD的中点,故可得出S ₃=S△AOB+S△COD=1/2S△ABD+1/2S△BCD=1/2(S△ABD+S△BCD)=1/2S;
(3)设▱ABCD中CD边上的高为h ₂,△PAB中AB边上高为h ₃,△PCD中CD边上的高为h4,再根据平行四边形的面积与三角形的面积公式求解即可;
(4)根据S△PBD=S四边形PBCD﹣S△BCD=S△PBC+S△PCD﹣S△BCD即可得出结论.
【解答】(1)设▱ABCD中BC边上的高为h ₁,CD边上的高为h ₂,
∵S▱ABCD=BC•h ₁=CD•h2=S,
S△BCM=1/2BC•h ₁=1/2S,S△BCD=1/2CD•h ₂=1/2S,
∴S ₁=1/2S,S₁=S₂(或相等).
故答案为:1/2;S₁=S₂;
(2)S₃=1/2S
理由:∵O为AC、BD的中点,
∴S₃=S△AOB+S△COD=1/2S△ABD+1/2S△BCD=1/2(S△ABD+S△BCD)=1/2S;
(3)设▱ABCD中CD边上的高为h2,△ABP中AB边上高为h₃,△PCD中CD边上的高为h4,
∵AB∥CD,∴h₃+h4=h₂,
∴S△PAB+S△PCD=1/2AB•h3+1/2CD•h4=1/2AB(h3+h4)1/2AB•h2=1/2S,即S′+S″=1/2S;
故答案为:S′+S″=1/2S;
(4)∵S△PAB+S△PCD=1/2S=S△BCD,S△PAB=3,S△PBC=7,
∴S△PBD=S四边形PBCD﹣S△BCD=S△PBC+S△PCD﹣S△BCD,即S△PBD=7+(1/2S﹣3)﹣1/2S=7﹣3=4.
【点评】本题考查的是平行四边形的性质,熟知平行四边形及三角形的面积公式是解答此题的关键.

类型3 条件不明确分类讨论求解
4.在平行四边形ABCD中,AB=4,BC=5,过点A作AE垂直直线BC于点E,AE=2√3.
(1)平行四边形ABCD的面积为_______ ;
(2)若再过点A作AF垂直于直线CD于点F,求CE+CF得值.
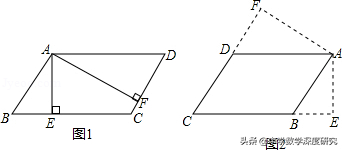
【分析】(1)由平行四边形的面积公式进行计算;
(2)根据平行四边形面积求出AE和AF,有两种情况,求出BE、DF的值,求出CE和CF的值,相加即可得出答案.
【解答】(1)如图,∵BC=5,过点A作AE垂直直线BC于点E,,
∴平行四边形ABCD的面积为:BC•AE=5×2√3=10√3;
故填:10√3;
(2)∵四边形ABCD是平行四边形,
∴AB=CD=4,BC=AD=5.
①由平行四边形面积公式得:BC×AE=CD×AF=10,则AF=5√3/2.
在Rt△ABE和Rt△ADF中,由勾股定理得:AB2=AE2+BE2,
把AB=4,AE=2√3代入求出BE=2,
同理DF=5/2<4,即F在线段DC上(如图1),
∴CE=5﹣2=3,CF=4﹣5/2=3/2,
即CE+CF=3+3/2=4.5,
②如图:∵AB=4,AE=2√3,在△ABE中,由勾股定理得:BE=2,
同理DF=5/2.则CE=BC+BE=5+2=7,CF=CD+DF=4+5/2=6.5,
∴CE+CF=7+6.5=13.5;
故答案为:4.5或13.5.
【点评】本题考查了平行四边形性质,勾股定理的应用,主要培养学生的理解能力和计算能力,注意:要分类讨论.










